반응형
1. 범용 함수(Universal Function) _ufunc
- Numpy 배열의 연산을 빠르게 만드는 핵심이다.
- 벡터화 : 벡터화를 통해 데이터를 규격화하고, 프로세스를 단순화 한다.
- 즉 데이터를 정규화 된 형식으로 사용하여 효율을 높인다.
- 프로세스를 압축하여 프로그램을 간단하게 만들 수 있다.
np.add()
import numpy as np
a = np.add([1,2,3,4,5],[1,2,3,4,5])
print(a)
- np.add는 두 배열의 원소별 합을 계산하는 ufunc
np.add.reduce() : 배열을 축소, 주어진 배열의 각 축에 대해 덧셈을 수행
b = np.array([[1,2,3],[4,5,6]])
print(np.add.reduce(b))
print(np.add.reduce(a))
print(np.add.reduce(b,axis = 1))
- 첫 번째 열: 1 + 4 = 5
두 번째 열: 2 + 5 = 7
세 번째 열: 3 + 6 = 9
- a처럼 1차원 배열에서는 모든 원소의 값을 더한 값을 반환한다. (30)
- axis를 1로 설정할 경우에는 각 행에 있는 값을 더해 결과를 1차원 배열로 반환한다.
np.add accumulate () : 누적 연산(덧셈)을 수행한다
np.multiply.accumulate() : 누적 연산(곱셈)을 수행한다
print('a=', a)
print('b=', b)
print('------accumulate-------')
print(np.add.accumulate(a))
print(np.add.accumulate(b))
print('------multiply---------')
print(np.multiply.accumulate(a))
print(np.multiply.accumulate(b))
np.add.reduceat() : 배열의 특정 구간을 선택하여 그 구간의 원소들을 합산하는 기능
arr = np.arange(16.0).reshape((4,4))
print(arr)
a = np.add.reduceat(arr, [0, 3, 1, 2, 0])
print(a)[[ 0. 1. 2. 3.] -> 행렬 arr
[ 4. 5. 6. 7.]
[ 8. 9. 10. 11.]
[12. 13. 14. 15.]]
[[12. 15. 18. 21.] // [0:3]의 행을 더한 것 (0행, 1,행,2행)
[12. 13. 14. 15.] // [3:1] 는 옳지 않은 범위이다 -> 1행만 반환
[ 4. 5. 6. 7.] // [1:2] 의 행을 더한 것(즉, 1행)
[ 8. 9. 10. 11.] // [2:0]은 옳지 않은 범위 -> 2행만 반환
[24. 28. 32. 36.]] // [0:] 은 전체 범위를 의미한다 -> 전체 행의 합
numpy.subtract() : 두 배열 간의 뺄셈 연산을 수행하는 방식
print(np.subtract(1.0,4.0))
arr = np.arange(9.0).reshape((3,3))
print(arr)
arr1 = np.arange(3.0)
print(arr1)
print(np.subtract(arr,arr1))-3.0 // np.subtract는 뺄셈 연산을 수행하는 함수이다.
[[0. 1. 2.]
[3. 4. 5.]
[6. 7. 8.]]
[0. 1. 2.]
// arr에서 arr1을 뺀다. -> arr는 2차원 arr1은 1차원이지만 브로드캐스팅을 통해 연산 수행이 가능하다.
[[0. 0. 0.]
[3. 3. 3.]
[6. 6. 6.]]
np.power() : 거듭 제곱을 수행하는 함수
arr1 = np.array(range(6))
print(arr1)
arr2 = np.power(arr1,3)
print(arr2)[0 1 2 3 4 5] // arr1
[ 0 1 8 27 64 125] // arr1의 각 요소를 3배수 한 결과
sin 함수를 이용하여 sin 함수 그래프를 그려보자
-> numpy.sin : 주어진 각도를 입력받아 해당 각도의 사인 값을 계산한다.
-> numpy.deg2rad() : 주어진 각도를 라디안 값으로 변환
print(np.sin(np.pi/2))
import matplotlib.pyplot as plt
arr = np.linspace(-np.pi,np.pi,1000)
plt.plot(arr,np.sin(arr))
plt.show()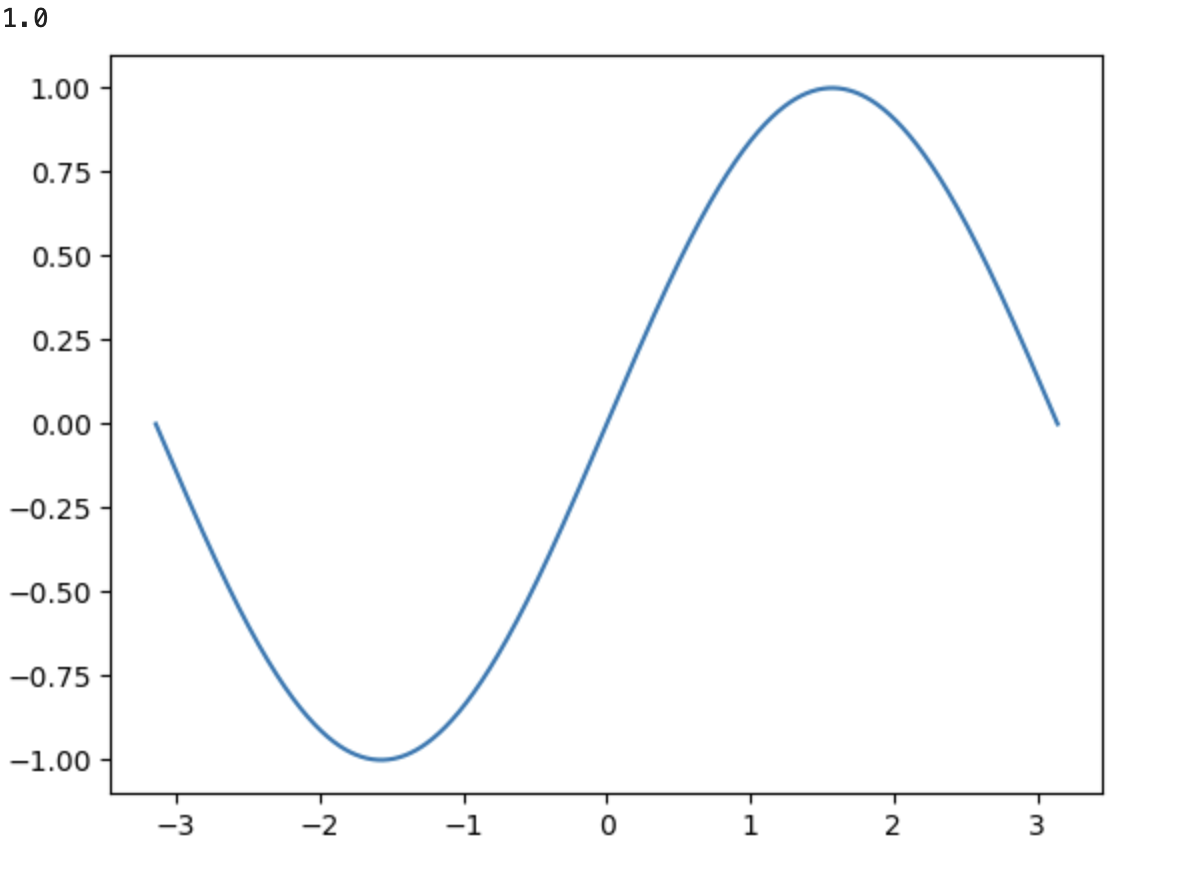
sin(np.pi/2)의 결과값을 확인해보면 sin 함수가 사인 값을 잘 계산해줬음을 확인 할 수 있다.
-pi 부터 pi 까지의 구간을 1000개로 나누어주고 각각의 값에 대한 사인값을 나타내는 그래프를 그려주었다.
* linspace 함수에서 사이 값을 개수를 충분히 크게 해주면 매끄럽지 못한 울퉁불퉁한 그래프가 나온다.
반응형

